수의 정확도, 오차#
강좌: 수치해석
유효 숫자#
과학 계산에서 수치는 실수 체계로 정의할 수 있다.
Fig. 2 실수 체계 (From wikimedia.org)#
매우 긴 숫자를 다루는 것은 현실적으로 어려우며, 유효 숫자 로 계산한다. 예를 들어 \(\pi\) 는 다음과 같은 4자리 유효 숫자로 표현할 수 있다.
import numpy as np
# 4 자리 유효숫자
np.round(np.pi, decimals=3)
3.142
실수를 표현하는 방식으로는 Decimal Notataion 과 Scientific Notation 이 있다.
# Decimal notation
print(r"Decimal notation of $\pi$: {:.3f}".format(np.pi))
# Scientific notataion
print(r"Scientific notation of $\pi$: {:e}".format(np.pi))
Decimal notation of $\pi$: 3.142
Scientific notation of $\pi$: 3.141593e+00
Note
컴퓨터도 모든 유효숫자를 저장할 수 없다.
오차#
컴퓨터 계산 과정에서 2가지 오차가 존재한다.
Round-off Erorr: 숫자 표기 한계로 반올림에 의한 오차
Truncation Error: 계산 과정에서 절단애 의한 오차
즉 수치해석 결과는 엄밀해는 다음 관계를 갖는다.
오차의 표현#
다음 수치 실험 값을 비교해보자.
\(C_l\) |
\(C_d\) |
|
|---|---|---|
실험 |
0.3501 |
0.0223 |
계산 |
0.3470 |
0.0201 |
\(C_l\) 과 \(C_d\)에 대한 오차를 계산해보면 다음과 같다.
\(C_l\) |
\(C_d\) |
|
|---|---|---|
\(\epsilon\) |
0.0031 |
0.0022 |
(절대) 오차 \(\epsilon\) 만 비교해보면 \(C_d\) 의 정확도가 더 높은 것 같다.
그러나 수치 크기에 대한 오차가 없으므로 다음과 같은 상대 오차를 정의한다.
참값을 아는 경우 참 상대오차 \(\epsilon_t\)를 사용할 수 있다.
위 예제에서 상대오차는 다음과 같다.
\(C_l\) |
\(C_d\) |
|
|---|---|---|
\(\epsilon_t\) |
0.89% |
9.9% |
즉, \(C_l\)의 상대오차가 더 작다.
다만 실제의 경우 참값을 모르는 경우가 많으므로 근사값을 기준으로 한 \(\epsilon_a\)를 사용한다.
\(e^x\) 근사 계산 예제#
Taylor expansion (Maclaurin expansion)을 사용하면 \(e^x\) 는 다음과 같이 근사할 수 있다.
\(|x| < 1\) 인 경우, 이전 항이 그 다음항보다 크다. n번째 항 까지만 계산할 경우 오차의 크기는 다음과 같다.
두번째항 까지만 근사하면 아래와 같다.
\(x=0.5\) 에 대해 절대오차는 다음과 같다.
np.exp(0.5) - (1.5)
0.1487212707001282
상대 오차는 다음과 같다.
(np.exp(0.5) - (1.5)) / np.exp(0.5)*100
9.02040104310499
참값 \(e^{0.5}\)를 모르는 경우 이전 근사값 (첫번째 항만 근사)와 현재 근사값간의 차이를 근사 오차 Error (appox) 로 해서 상대오차를 계산한다.
(1.5 - 1) / (1.5)*100
33.33333333333333
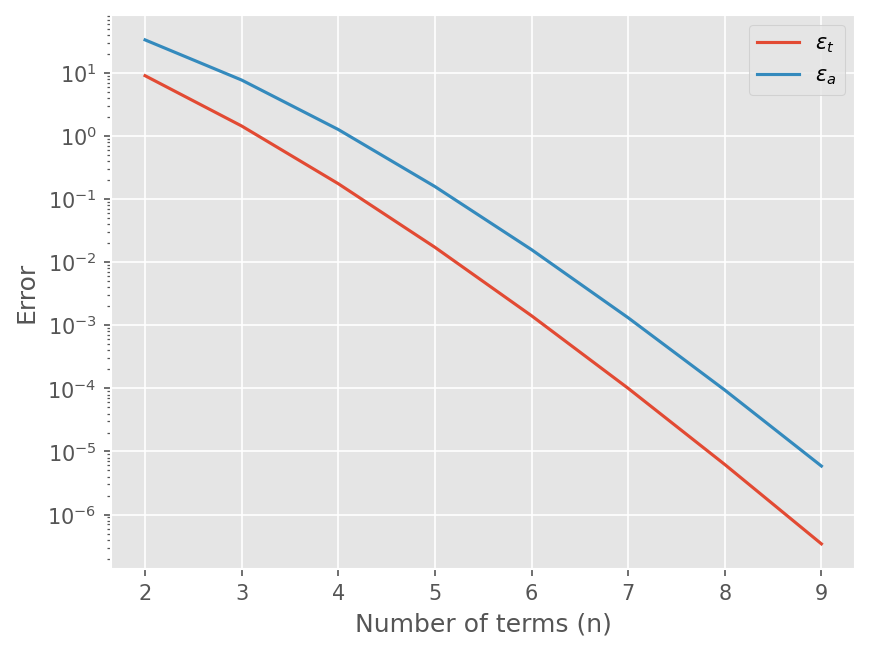
근사식의 항을 늘리면서 두 상대오차를 계산하면 다음과 같다.
def factorial(n):
""" Factorial 계산
Parameters
----------
n : integer
n
"""
fac = 1
for i in range(1, n+1):
fac *= i
return fac
def approx_exp(n, x):
""" Exponential 함수 근사
Parameters
n : integer
항의 계수
x : float
값
"""
exp = 0
for i in range(n):
exp += 1/factorial(i)*x**i
## Pythoniac
# exp = sum([factorial(i)*x**i for i in range(n)])
return exp
def epsilon_t(n, x):
"""참 상대오차 계산
Parameters
----------
n : integer
항의 계수
x : float
값
"""
# Exact
exact = np.exp(x)
# Approx
approx = approx_exp(n, x)
return (exact - approx)/exact*100
epsilon_t(2, 0.5)
9.02040104310499
def epsilon_a(n, x):
"""근사 상대오차 계산
Parameters
----------
n : integer
항의 계수
x : float
값
"""
# n번째와 n-1번째 항까지 근사값
approx_n = approx_exp(n, x)
approx_n1 = approx_exp(n-1, x)
return (approx_n - approx_n1) / approx_n*100
epsilon_a(2, 0.5)
33.33333333333333
Note
Docstring (문서화)는 매우 중요하다. 규칙을 사용할 필요가 있다. 이 강의에서는 Numpydoc 를 따른다.
x = 0.5
err_t = []
err_a = []
for n in range(2, 10):
err_tn = epsilon_t(n, x)
err_an = epsilon_a(n, x)
print(r"terms {}, $\epsilon_t$ : {:.3e}, $\epsilon_a$ : {:.3e}".format(n, err_tn, err_an))
err_t.append(err_tn)
err_a.append(err_an)
terms 2, $\epsilon_t$ : 9.020e+00, $\epsilon_a$ : 3.333e+01
terms 3, $\epsilon_t$ : 1.439e+00, $\epsilon_a$ : 7.692e+00
terms 4, $\epsilon_t$ : 1.752e-01, $\epsilon_a$ : 1.266e+00
terms 5, $\epsilon_t$ : 1.721e-02, $\epsilon_a$ : 1.580e-01
terms 6, $\epsilon_t$ : 1.416e-03, $\epsilon_a$ : 1.580e-02
terms 7, $\epsilon_t$ : 1.002e-04, $\epsilon_a$ : 1.316e-03
terms 8, $\epsilon_t$ : 6.220e-06, $\epsilon_a$ : 9.402e-05
terms 9, $\epsilon_t$ : 3.435e-07, $\epsilon_a$ : 5.876e-06
%matplotlib inline
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150
plt.semilogy(range(2, 10), err_t)
plt.semilogy(range(2, 10), err_a)
plt.xlabel("Number of terms (n)")
plt.ylabel("Error")
plt.legend(["$\epsilon_t$", "$\epsilon_a$"])
<matplotlib.legend.Legend at 0x7f9f26415050>
DIY #1#
\(\cos(x)\) 과 \(\sin(x)\) 함수는 Taylor expansion에 의해 다음과 같이 표현할 수 있다.
여기서 \(x\)의 단위는 radian이다.
\(x\)가 5도 각도일 때 근사항의 갯수에 따른 절대오차, 참 상대오차, 근사 상대 오차를 구하고 이를 그래프로 표현하시오.
Tip) np.deg2rad, np.rad2deg 함수 참고할 것
Round-off Error#
컴퓨터에수 수의 표현#
컴퓨터는 여러개의 스위치(?, bit)를 이용해서 2진법으로 숫자를 표현한다.
Fig. 3 2진법 (From wikimedia.org)#
크게 정수 (Integer) 와 부동 소숫점 (floating point) 로 표현한다.
정수#
16bit 컴퓨터에서 10진법으로 표현할 수 있는 정수의 범위를 생각해보자.
가장 큰 수
즉 (-32,767, 32767) 까지 수를 표현할 수 있다.
Fixed Point vs Floating Point#
Fixed Point는 Decimcal notation 처럼 정수부와 소수부로 구분해서 표현하는 방식이다.
예를 들어 16bit 컴퓨터에서 1개의 bit는 부호, 7개는 정수부, 8개는 소수부로 표현하는 방식이다. 수의 표현에 많은 한계가 있다.
Floating point (부동소숫점)은 Scientific notation과 같이 부호, 지수부 (exponent), 가수부 (mantissa or fraction) 로 구분한다.
정규화를 위해 \(1/b \leq m < 1\) 로 제한된다.
IEEE754 규격을 가장 널리 사용하는 표준이다.
Fig. 4 Floating Point (From Wikipedia)#
7bit floating point#
다음과 같이 표현한다.
첫번째 bit : 부호
2~4 번째 bit : 지수의 부호 (1 bit), 지수의 크기 (2bit)
5~7 번재 bit : 가수 (3bit)
가장 작은 양수: \(0111100_{(2)} = +2^{-(1\times2 + 1)}\times(1\times2^{-1} + 0\times2^{-2} + 0\times2^{-3}) = +0.5\times2^{-3}=0.0625\)
그 다음으로 표현 가능한 수는 아래와 같다.
즉 \(0.015625(=2^{-6})\) 씩 증가시킬 수 있다.
그 다음 큰 수는 지수를 증가시켜야 한다.
그 다음 큰 수는 아래와 같다.
즉 \(0.03215(=2^{-5})\) 씩 증가시킬 수 있다.
가장 큰 수는 다음과 같다.
Underflow, Overflow, Machine epsilon#
위 예제와 같이 floating point는 넓은 범위의 숫자를 표현할 수 있으나 모든 숫자를 표현할 수 없다.
Fig. 5 Distriution of Floating Point (From Wikipedia)#
다음 3가지 특징이 있다.
표현할 수 있는 수의 한계가 있음
Overflow: 허용된 범위를 벗어난 큰 수 표현하지 못함
Underflow: 매우 작은 숫자를 표현하지 못함
주어진 범위 안에넛 표현할 수 있는 수자의 개수는 유한함
근사값으로 표현 (Quantizing error, round-off error)
Machine epsilon
수 사이의 간격 \(\Delta x\)는 수의 크가기 증가함에 따라 커짐
단정밀도, 배정밀도#
일반적으로 컴퓨터의 기본 단위 (word)는 32비트로 한다. 이를 기준으로 해서 다음과 같은 정밀도를 생각한다.
정밀도 |
크기 |
|---|---|
단정밀도 |
32bit |
배정밀도 |
64bit |
반정밀도 |
16bit |
FP32, FP64, FP16 등으로 표현하기도 한다. 현대 수치해석에서 기본 단위는 배정밀도이다.
Numpy 에서는 np.float32, np.float64, np.float16 등으로 표현한다.
np.finfo 이용하면 여러 특징을 살펴볼 수 있다.
np.finfo(1.0)
finfo(resolution=1e-15, min=-1.7976931348623157e+308, max=1.7976931348623157e+308, dtype=float64)
연산의 오류#
연산에서 매우 작은 수 또는 매우 큰 수는 표현할 수 없어서 오류가 발생한다
# FP16 숫자 특징
print(np.finfo(np.float16))
Machine parameters for float16
---------------------------------------------------------------
precision = 3 resolution = 1.00040e-03
machep = -10 eps = 9.76562e-04
negep = -11 epsneg = 4.88281e-04
minexp = -14 tiny = 6.10352e-05
maxexp = 16 max = 6.55040e+04
nexp = 5 min = -max
smallest_normal = 6.10352e-05 smallest_subnormal = 5.96046e-08
---------------------------------------------------------------
# FP16에서 매우 작은 수 더하기
a = np.float16(1.0)
np.float16(a + 9e-4)
1.001
# FP16에서 비슷한 크기의 숫자 빼기 (밸샘의 무효화)
a = np.float16(0.5)
b = np.float16(0.4999)
np.float16(b -a)
0.0
# Overflow
a = np.float16(4e4)
b = np.float16(3e4)
np.float16(a + b)
/tmp/ipykernel_296/3507621214.py:5: RuntimeWarning: overflow encountered in scalar add
np.float16(a + b)
inf
# Underflow
a = np.float16(1e-7)
np.float16(a/10)
0.0
DIY #2#
단정밀도, 배정밀도에 대해서 뺄샘의 무효화, Overflow, Underflow 상황을 만들어 보시오.